검정(test)
특정 분포를 기준으로 했을 때 유의성이 있는가 판별하는 것.
1. 카이제곱검정(Chi-squares)
그룹간 관찰빈도와 기대빈도를 통해 두 집단간의 차이가 유의한가를 판별하는 방법. 카이검정은 범주형 변수일 경우 두 독립군간의 비교를 할 때 쓰인다.(연속형 변수인 두 독립군 간의 비교는 t-test 사용)
귀무가설(H0)과 대립가설(H1)
이 가설들은 기본적으로 통계학에서 처음부터 버릴 것을 예상하는 가설이다.
귀무가설은 앞으로 내가 검정해야 하는 것이다. (내가 궁금한 것/관찰한 것 ex-주사위 프로그램 검정 (기댓값과 달리 랜덤하게 나오는가?) 기댓값과 같이 유사한 구조로 나오는가? 등) 일단 귀무가설이 옳다는 가정하에 시작하나, 예상이기 때문에 진실일 가능성이 적다.
대립가설은 귀무가설이 기각될 때 받아들여지는 가설이다.
유의확률(pvalue)
통계적으로 유의하다면 우연이 아닌 의미가 있다는 뜻으로, 유의확률(pvalue)가 작을수록 좋다. 유의확률은 기본적으로 귀무가설이 맞다고 가정할 때, 귀무가설이 실제로 옮음에도 기각할 오류(기각할 때 따르는 위험부담)이다. 위험부담이 클수록 귀무가설이 맞다는 소리. 따라서,
pvalue< 0.05 라면, 신뢰수준하에서 유의한 관계로, 대립가설 채택한다.
pvalue< 0.05 라면, 신뢰수준하에서 무의미한 관계로, 귀무가설 채택한다.
코드는 관측값(입력값) data1과 기댓값(예상값)data2를 두고 chisquare를 한다.
카이제곱검정(Chi-squares)은 적합도 검정과 독립 검정으로 나뉜다.
1) 적합도 검정(Goodness of fit test)
관측된 데이터가 예측한 분포를 따르는지 검정하는 방법 ex) 게임이 공정한지 여러 게임으로 검정
chisquare : 카이제곱 검정은 이산형과 이산형 변수가 서로 상관관계가 있는지 없는지를 확인한다.
stats.chisquare 검정통계량과 pvalue를 얻을 수 있다.
#관측값
data1 = [86,36,30,19]
#기대값
data2 = [42.75,42.75,42.75,42.75]
chis = stats.chisquare(data1,data2)
chis
#결과 출력
statistic,pvalue = chis #zip 형태처럼 두개의 변수에 값을 각각 할당
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")▼연습문제
문제1. 주사위를 n번 던졌을 때 나오는 데이터의 차이가 있는지 없는지 알아보기
귀무가설 : 두 변수는 연관성이 없다, 차이가 없다. => 주사위 프로그램은 제대로 만들어졌다.
대립가설 : 두 변수는 연관성이 있다, 차이가 있다. => 주사위 프로그램은 문제가 있다.
#scipy 통계 라이브러리
from scipy import stats
#임의의 데이터 생성
data1 = [4,6,17,16,8,9]
print('주사위 던진 횟수 : ',sum(data1)) #60회chisquare : 카이제곱 검정은 이산형과 이산형 변수가 서로 상관관계가 있는지 없는지를 확인한다.
#관측값
data1 = [4,6,17,16,8,9]
#기대값
data2 = [10,10,10,10,10,10]data1은 내가 던진 주사위의 데이터다. 주사위 프로그램 실험을 위해 귀무가설로 "(확률상 나오기 힘든)임의의 기댓값이 내가 만들어낸 프로그램의 관픅값과 연관성이 있는가?" 를 판단해보자. 만약 관련이 있으면 주사위 프로그램에 문제가 있는 것이다. 동일한게 6번 나오는건 극히 드물기 때문에....
수식으로는 겁나 복잡하지만 코딩으로는 한줄.
#검정통계량과 p-value
chis = stats.chisquare(data1,data2)
chis
깔끔하게 보기 위해 if문으로 결과값을 내보자.
#결과 출력
statistic,pvalue = chis #zip 형태처럼 두개의 변수에 값을 각각 할당
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")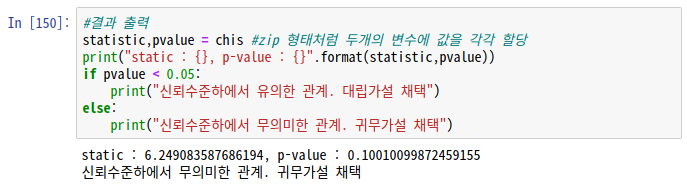
p-value가 0.05보다 작으므로 신뢰수준 하에서 유의한 관계가 있다.
귀무가설 기각, 대립가설 채택
따라서 data1과 data2는 차이가 있다.
문제2. 다음표는 완두콩의 잡종의 분류에 대한 관측도수와 기대치이다. 이 데이터는 유전의 이론적으로 모형에 부합된다고 할 수 있는가? (유의수준 : 0.05)
#관측값
data1 = [322,108,98,32]
#기대값
data2 = [315,105,105,35]chis = stats.chisquare(data1,data2)
chis
#결과 출력
statistic,pvalue = chis #zip 형태처럼 두개의 변수에 값을 각각 할당
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")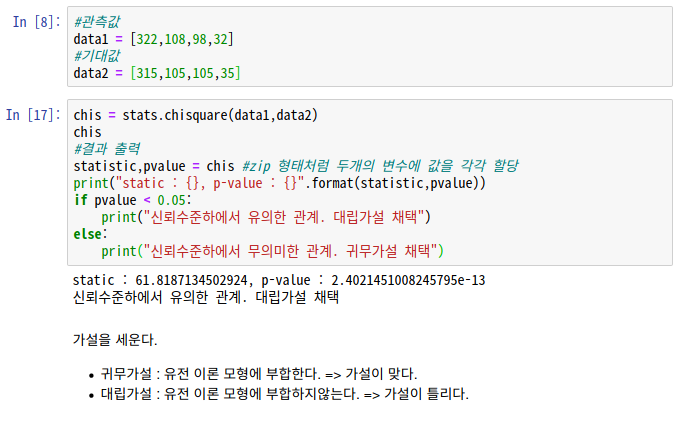
#관측값
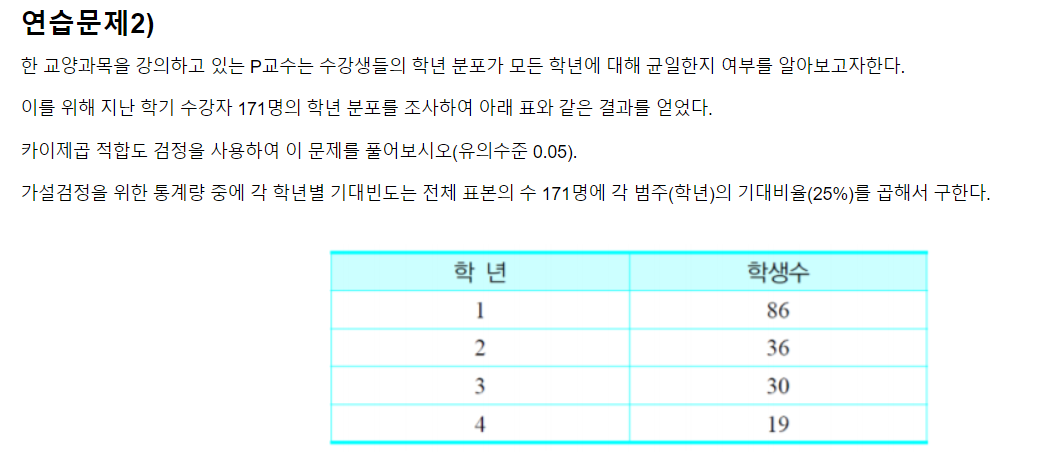
data1 = [86,36,30,19]
#기대값
data2 = [42.75,42.75,42.75,42.75]
chis = stats.chisquare(data1,data2)
chis
#결과 출력
statistic,pvalue = chis #zip 형태처럼 두개의 변수에 값을 각각 할당
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")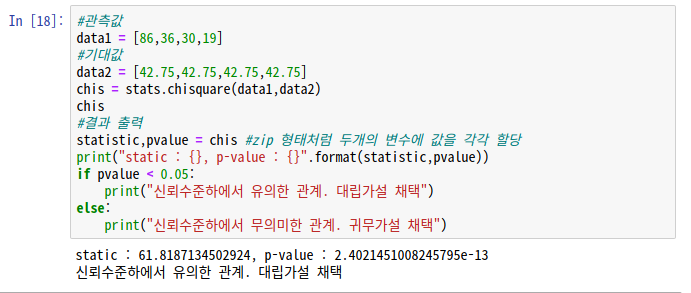
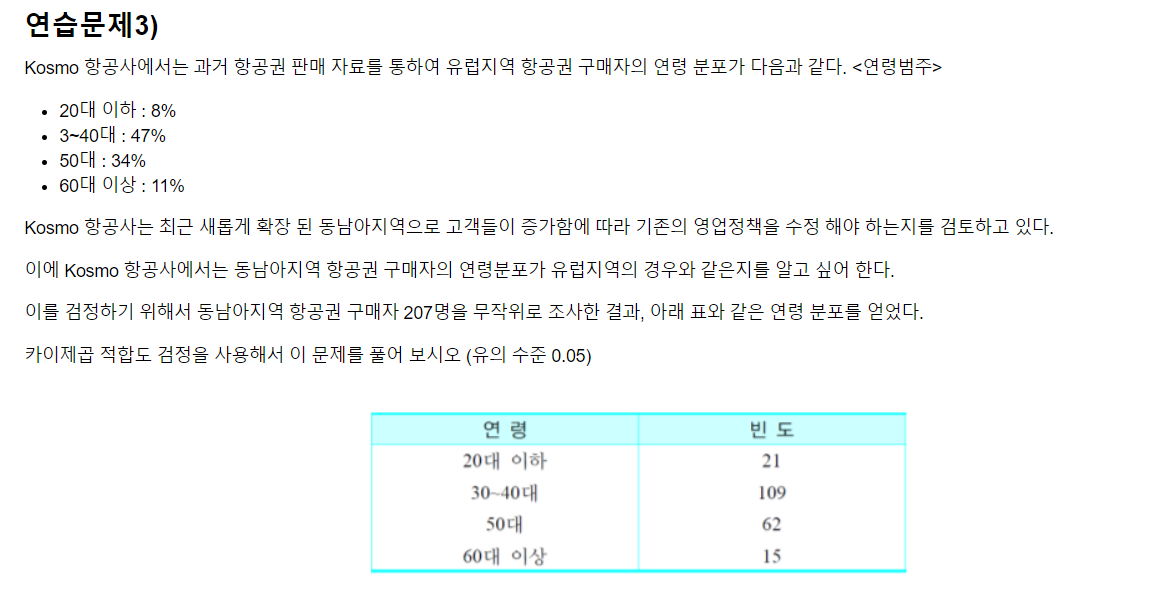
- 귀무가설 : 동남아지역 항공권 구매자의 연령분포가 유럽지역의 경우와 같다.
- 대립가설 : 동남아지역 항공권 구매자의 연령분포가 유럽지역의 경우와 다르다.
chis = stats.chisquare(data1,data2)
chis
#결과 출력
statistic,pvalue = chis #zip 형태처럼 두개의 변수에 값을 각각 할당
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")전체표본의수: 207
기대값: [16.56 97.29 70.38 22.77]
import numpy as np
#관측값
data1 = np.array([21,109,62,15])
#전체표본수
total = np.sum(data1)
print('전체표본의수:',total)
#기대비율
e_per = np.array([0.08,0.47,0.34,0.11])
#기대값구하기
#기대값 :기대치 = 전체표본의수*기대비율
data2 = total*e_per
print('기대값:',data2)static : 6.249083587686194, p-value : 0.10010099872459155
신뢰수준하에서 무의미한 관계. 귀무가설 채택
2) 독립성 검정(Test of independence)
관측값들이 다수의 인자들에 의해 분할 되어 있는 경우 그 인자들의 관찰 값에 영향을 주고 있는지 아닌지를 검정하는 방법. 여러 범주를 가지는 두 개의 변수가 서로 독립적인지 또는 관련이 있는지를 분석한다. ex) 선호하는 음식의 종류와 연령이 서로 관령성이 있는지를 알고 싶을 때
독립성 검정은 귀무가설 : 독립이다. / 대립가설 : 독립이 아니다. 를 의미한다. 여기서 독립이라는 의미는 인과관계 혹은 연관이 없다는 말이 될 수 있다. (교육수준 과 수업이 연관관계가 있는지 없는지,나이와 정당선호도가 연관이 되는지 없는지)
obs = np.array([[5,15],[10,20]])numpy와 아주 밀접한 관계가 있다.
chi2_contingency(독립성 검정) : 카이제곱 통계량, p-value, 자유도 등을 return
#독립성검정
statistic,pvalue,_,_ = stats.chi2_contingency(obs)
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택"),_,_는 굳이 넣지 않은 자유도나 타 조건들을 의미한다.
▼연습문제
문제1. 두 개의 광고 서비스를 통해 각각 유입된 사용자들의 이용률을 독립성 검정을 이용해 분석해라.
- 귀무가설 : 모집단 sample A와 모집단 sample B의 지속 이용 전환율은 다르지 않다.
- 대립가설 : 모집단 sample A와 모집단 sample B의 지속 이용 전환율은 다르다.
data1 = np.array([40,165]) # 지속이용사용자수 #해지한 사용자 수
data2 = np.array([62,228])
print("유입사용자수 A : {}, 지속사용자수 : {}, 지속이용전환율(mean)={:.3f}".format(
np.sum(data1), #전체 유입
data1[0],
data1[0]/np.sum(data1) #전체유입 대비 남은사람 비율
))
print("유입사용자수 B : {}, 지속사용자수 : {}, 지속이용전환율(mean)={:.3f}".format(
np.sum(data2),
data2[0],
data2[0]/np.sum(data2)
))
#카이제곱검정 : 독립성 검정
statistic,pvalue,_,_ = stats.chi2_contingency(obs)
print("static : {}, p-value : {}".format(statistic,pvalue))
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")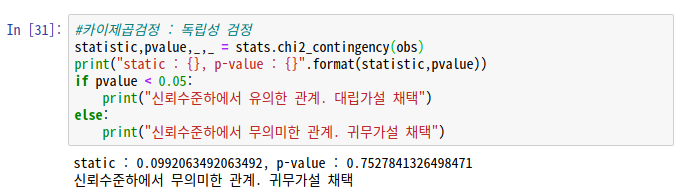
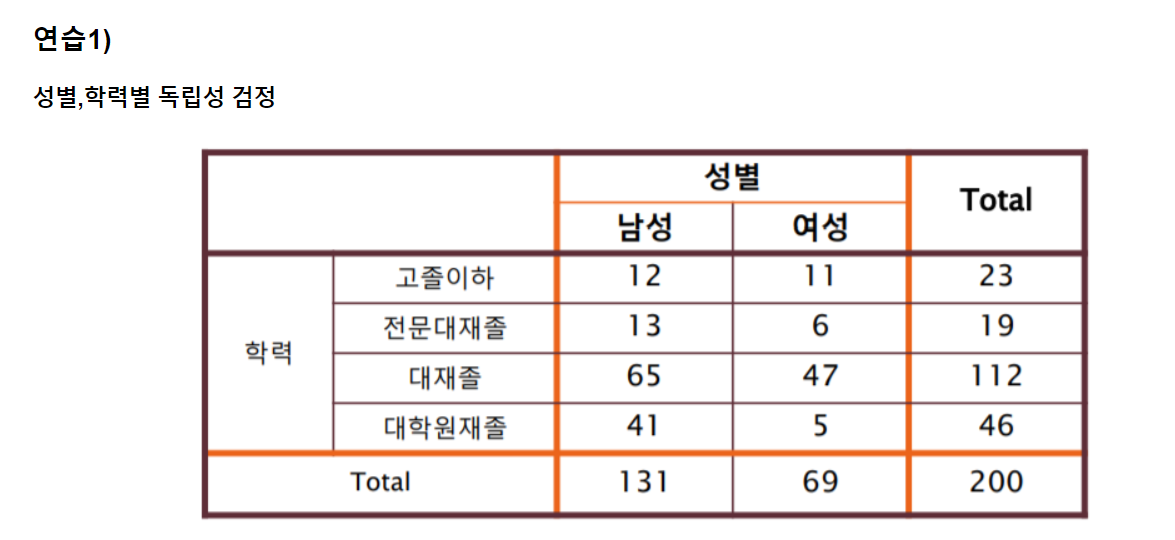
가설 ) 성별과 학력이 서로 관계가 있다고 말할 수 있는가? (유의수준 0.05)
- 귀무가설 : 두 변수는 독립적인 관계이다. 학력에 따른 성별 비율의 차이는 없다
- 대립가설 : 두 변수는 독립적인 관계가 아니다. 학력에 따른 성별 비율의 차이는 있다.
data1 = np.array([12,13,65,41])
data2 = np.array([11,6,47,5])
statistic,pvalue,df,e =stats.chi2_contingency([data1,data2])
print(statistic)
print(pvalue)# 대립가설 채택t검정 : 두 집단간의 평균을 비교할 때 사용하는 방법
1) 단일표본 t-test : 한 집단 평균 검정
- 하나의 데이터 집단의 평균과 비교하고자 하는 관측치를 통해 차이를 검정하는 방법
- 데이터 집단의 평균과 거리가 멀 수록 p-value 유의수준의 값이 떨어진다.
- stats.ttest_1samp() 이용
ttest_1samp : 모집단 M와 x_1
표본의 평균이 모집단의 평균과 일치한다”라는 귀무가설을 확인하는 방법
ex) 키 : 표본 1개랑 모집단 평균이랑 같은지? 키가 175인가?
one_sample = [177.3, 182.7, 169.6, 176.3, 180.3, 179.4, 178.5, 177.2, 181.8, 176.5]
print(mean(one_sample)) # 177.96
result = stats.ttest_1samp(one_sample, 175.6) # 비교집단, 관측치
print('t검정 통계량 = %.3f, pvalue = %.3f'%(one_sample_result))
# t검정 통계량 = 2.296, pvalue = 0.0723f는 셋째자리에서 반올림
2) 독립표본 t-test : 두개의 집단 평균 검정
- 두 데이터 집단간의 평균을 서로 비교해서 그 차이를 검정ㅎ는 방법
- stats.ttest_ind(x,y) 이용
ttest_ind : x_1 과 x_2
2개 집단에서 표본을 수집했을 때, 두 집단의 평균이 서로 일치한다”라는 귀무가설을 확인하는 방법
ex) 신발사이즈, 두집단의 평균(남자 평균, 여자평균)
female = [63.8, 56.4, 55.2, 58.5, 64.0, 51.6, 54.6, 71.0]
male = [75.5, 83.9, 75.7, 72.5, 56.2, 73.4, 67.7, 87.9]
result = stats.ttest_ind(male, female)
print("t검정 통계량: %.3f, pvalue=%.3f"%(result))
# t검정 통계량 = 3.588, pvalue = 0.0033) 대응표본 t-test : 같은 집단의 대응되는 두 변수를 비교
- before 와 after의 변화가 얼마나 대응 되는지(국어점수, 수학점수 또는 사전점수 사후점수 등)
- stats.ttest_rel(x,y) 이용
ttest_rel : A -> B
baseline = [67.2, 67.4, 71.5, 77.6, 86.0, 89.1, 59.5, 81.9, 105.5]
follow_up = [62.4, 64.6, 70.4, 62.6, 80.1, 73.2, 58.2, 71.0, 101.0]
paried_sample = stats.ttest_rel(baseline, follow_up)
print('t검정 통계량 = %.3f, pvalue = %.3f'%paired_sample)
# t검정 통계량 = 3.668, pvalue = 0.006출처 : blog.naver.com/nonamed0000/220908890568
▼연습문제
문제1) 귀무가설 : 학생들의 평균키는 175cm이다. 대립가설 : 학생들의 평균키는 175cm가 아니다.
np.random.seed(1) # 재현률 난수값을 고정할 때 사용
# np.random.normal(평균,표준편차)
heights = [180 + np.random.normal(0,5) for a in range(20)]
heights
#ttest_1samp : 독립표본 T검정 (이산형과 연속형 변수의 상관관계를 알고 싶을 때 )
# 175인지 아닌지 - 이산형 변수, 175는 늘어나는 수 즉 연속형 변수 라 할 수 있다.
result = stats.ttest_1samp(heights, 175)
print(result)
print("단일표본 T-검정 검정통계량: %.3f, pvalue: %.3f" % result)
if pvalue < 0.05:
print("대립가설 채택")
else:
print("귀무가설 채택")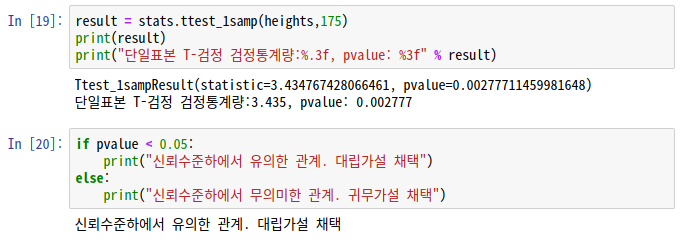

문제2) 다음 데이터의 표본이 모집단 평균과 비슷할까?
- 귀무가설 "표본의 평균이 모집단의 평균과 일치한다" 대립가설 "표본의 평균이 모집단의 평균과 일치하지 않는다"
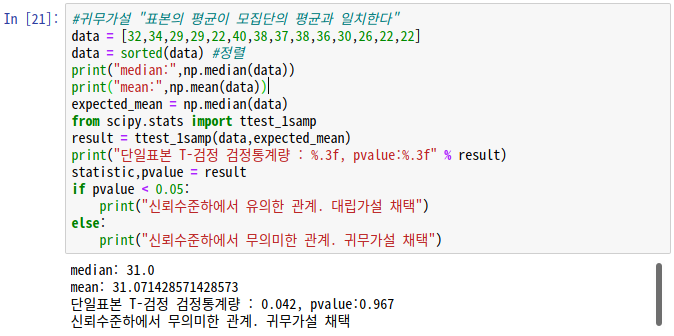
#귀무가설 "표본의 평균이 모집단의 평균과 일치한다"
data = [32,34,29,29,22,40,38,37,38,36,30,26,22,22]
data = sorted(data) #정렬
print("median:",np.median(data))
print("mean:",np.mean(data))
expected_mean = np.median(data)
from scipy.stats import ttest_1samp
result = ttest_1samp(data,expected_mean)
print("단일표본 T-검정 검정통계량 : %.3f, pvalue:%.3f" % result)
statistic,pvalue = result
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")뭐 당연히... 데이터는 똑같고 그걸로 평균내냐, 중간값내냐 차이라... 당연히 일치한다.
문제3) 그룹1과 그룹2에서 각각 학생들을 선택해서 평균키가 같은지 알고싶다.
#귀무가설 : 학생들의 평균키가 같지 않다.(상과관계가 없다.)
#대립가설 : 학생들의 평균키가 같지 않다.(내가 주장하고 싶은 것, 상관관계가 있다.)
np.random.seed(1)
group1=[170+np.random.normal(0,5) for a in range(20)] #170 근처의 값이 나오도록 설정한다.
group2=[175+np.random.normal(0,10) for a in range(20)] #175 근처의 값이 나오도록 설정한다.
print("group1의 평균 :",np.mean(group1))
print("group2의 평균 :",np.mean(group2))
result1 = stats.ttest_ind(group1,group2)
statistic,pvalue = result1
print("독립표본 T-검정 검정통계량 : %.3f, pvalue:%.3f" % result1)
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")
문제4) 남자와 여자의 신발사이즈의 평균이 같은지 다른지 선별하시오. -> 귀무가설 : 두집단의 평균이 같다
import pandas as pd
df = pd.read_excel('dataset/exam24.xlsx')
#남자가 1, 여자가2
df.head(5)
#번호 컬럼 삭제
df=df.drop(df.columns[0],axis=1)
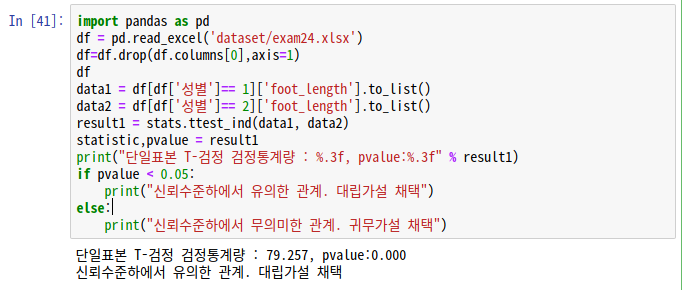
#data1과 data2에 각각 성별별로 발사이즈 넣기
data1 = df[df['성별']== 1]['foot_length'].to_list()
data2 = df[df['성별']== 2]['foot_length'].to_list()
result1 = stats.ttest_ind(data1, data2)
statistic,pvalue = result1
print("단일표본 T-검정 검정통계량 : %.3f, pvalue:%.3f" % result1)
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")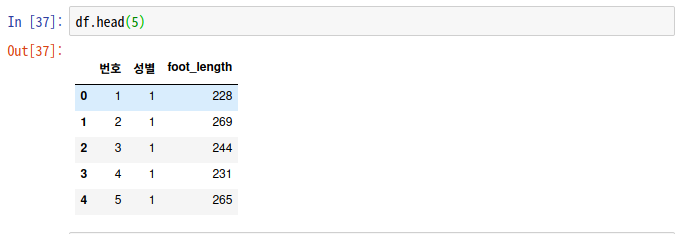
문제5) 어떤 회사에서 탈모약을 개발해서 임상실험을 하는 상황이다. 50명을 모집해서 6개월간 탈모약을 복용하게 했고, 복용 전과 후의 모발 수를 비교했다.
- 귀무가설 : 복용 후 모발 수가 복용 전보다 크지 않다
- 대립가설 : 복용 후 모발 수가 복용 전보다 크다.
import pandas as pd
df = pd.read_excel('dataset/탈모.xlsx')
df.head(5)
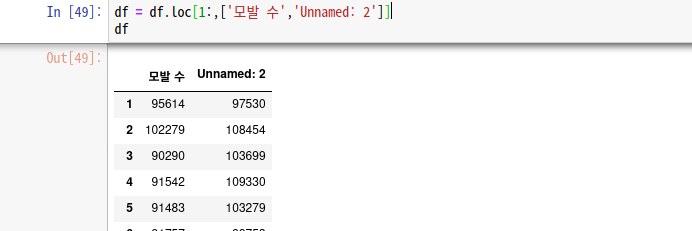
# 컬럼명이 있는 첫줄과 데이터를 제외한 모든값 잘라냄
df = df.loc[1:,['모발 수','Unnamed: 2']]
#컬럼명 맞게 바꿔주기
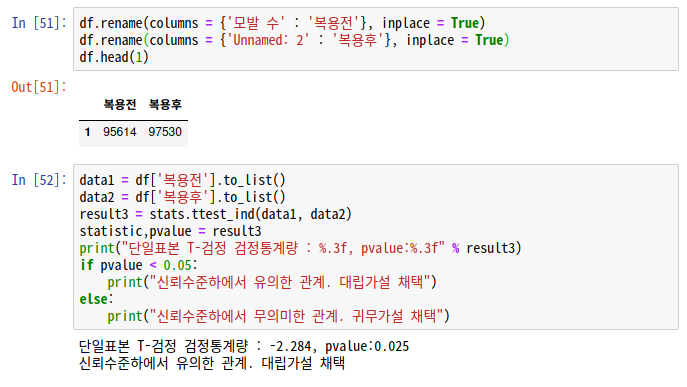
df.rename(columns = {'모발 수' : '복용전'}, inplace = True)
df.rename(columns = {'Unnamed: 2' : '복용후'}, inplace = True)
df.head(1)
data1 = df['복용전'].to_list()
data2 = df['복용후'].to_list()
result3 = stats.ttest_ind(data1, data2)
statistic,pvalue = result3
print("단일표본 T-검정 검정통계량 : %.3f, pvalue:%.3f" % result3)
if pvalue < 0.05:
print("신뢰수준하에서 유의한 관계. 대립가설 채택")
else:
print("신뢰수준하에서 무의미한 관계. 귀무가설 채택")빠트린 것! index가 0부터 안하니까 다시 reset 해줘야한다.
df.reset_index(drop=True)
np.random.seed()는 난수를 예측 가능하게 만든다.
원래 np.random.rand(4)로 4개의 랜덤한 array를 만든다고 했을 때, 4개가 랜덤으로 지정되고 실행을 시킬 때마다 다른 array가 나온다. 하지만 np.random.seed(1)를 하게 되면 고정되어 동일한 세트의 난수가 나타난다. -> seed라는 하나의 파라미터를 생성해서 똑같은 것을 불러오는 것. 괄호의 숫자는 키값과 비슷하다.
'[ Python ]' 카테고리의 다른 글
| [Python] 머신러닝 개념 잡기 (1) | 2020.11.06 |
|---|---|
| [Python] SciPy / 기초기술통계 / ANOVA(분산분석) / 회귀분석 (0) | 2020.11.02 |
| [Python] Pandas 기초 / groupby / 데이터프레임 Json으로 저장 / 실습(3) (0) | 2020.10.30 |
| [Python] Pandas 기초 / DataFrame / matplotlib / 실습(2) (0) | 2020.10.29 |
| [python] 주피터 노트북(jupyter notebook) 단축키 (0) | 2020.10.28 |