# 오늘은 전처리 맛보기만 해보자.
ANOVA (ANalysis Of VAriance; 분산 분석)
3개 이상 다수의 그룹간의 평균의 차이가 통계적으로 유의미 한지를 판단하기 위한 시험법. F분포를 이용한다.
▼ 카이제곱검정 vs T검정 vs ANOVA(분산검정)
연속형자료와 범주형 자료
- 연속형 : 키, 몸무게 등 수량화 가능한 자료.
- 범주형 : 성별, 혈액형, 치료반응 유무 등 수향화 할 수 없는 자료.
연속형 변수를 검정하는데에는 T검정과 ANOVA(분산분석) 이 사용되고, 범주형 변수를 검정할 경우 카이제곱검정과 피셔의 정확검정법을 사용할 수 있다.
- 상관분석 : 두 변수 간에 얼마나 상관이 있는가?선형관계인가?
- 회귀분석 : y=a+bx 관계식 구하기
| 카이제곱검정 | T검정 | ANOVA(분산검정) |
| 범주형 변수 | 연속형 변수 | |
| 두 변수간의 상관관계 측정할 때 | 두 그룹의 평균 차이를 볼 때 | 세 그룹 이상의 평균값 분석할 때 |
| 기대빈도를 두고, 관찰빈도가 통계적으로 유의미한지 측정 | 두 표본이 있는데 그 차이를 표본 오차로 한다. 표본 오차가 발생할 확률이 a<0.05로 유의미하면 대립가설 채택 | 세개 이상 표본이 있는데 각각의 평균이 동일하다는 가설을 검정. 분산이 모두 같다는 가정 하에 오차가 크면 대립가설 채택 |
| - 적합도 검정 : 관측된 데이터가 예측한 분포를 따르는지 검정 - 독립성 검정 : 관측값들이 다수의 인자들에 의해 분할되어 있는 경우, 그 인자들이 서로 독립적인지 또는 관련이 있는지 검정 |
- 단일표본 t검정 : 하나의 모집단의 평균값을 기준값과 비교 - 독립표본 t검정 : 서로 다른 두개의 그룹간의 평균 비교 - 대응표본 t검정 : 동일한 집단의 사전, 사후 평균 비교 |
- 일원분산분석 : 하나의 독립변수를 이용한 분산분석(수준 2개) 두 평균이 같은가 다른가? - 이원분산분석 : 두개의 독립변수를 이용한 분산분석(수준 여러개) 여러 요인들이 종속변수와 얼마만큼 관련이 있는가? - 다변량분산분석 : 종속변수가 여러개 |
| - 주사위 프로그램을 만들었다. 프로그램 관측한 값과 기대한 값(나올 수 없는 값)이 서로 상관관계가 있는가?(적합) - 완두콩 잡종을 분류하려고 한다. 이 관측데이터로 보아 이 데이터는 유전이론모형에 적합한가?(적합) - 학년별 인원에 대한 관측값으로 보아 학년 분포가 균일한가?(독립) - 교육수준과 성적이 연관관계가 있나?(독립) |
- 평균키가 175다, 아니다(단일) - 남자와 여자간의 소득 차이 비교(독립) - A그룹과 B그룹 학생들의 평균키가 같은지 비교(독립) - 임상실험에서 복용전과 복용후 결과 비교(대응) |
- 신입사원에게 4가지 각기 다른 교육 훈련 방법을 사용해서 가르치고 표준 시험을 치룬 결과가 다음과 같다. 기법간 차이가 있나?(일원) - 당뇨병과 관련된 정보와 당뇨병에 걸렸는지(1), 안걸렸는지(0)에 대한 환자데이터가 있다. 어떤 정보가 당뇨병이 걸릴 확률과 관련이 높은가?(이원) - 교과서의 차이가 학생들의 수학과 과학점수에 미치는 영향(다변량) |
1) 일원분산분석(One-way ANOVA)
[ 문제 ] 김부장이 4개의 각기 다른 신입사원 교육훈련 기법의 효과성을 평가하고자 한다. 새로 입사한 32명의 신입사원에게 4가지 기법을 임의로 적용시켜 교육을 시켰다. 한 달간의 훈련기간이 끝난 후 표준 시험을 쳤는데 그 점수는 아래와 같다. 4개의 교육훈련 기법간 차이가 있는가? 만약 있다면 어떻게 다른가?
-> 3개 이상의 대응표본을 비교해야 하므로 일원배치 분산분석 기법을 사용해야 한다.
- 귀무가설 : 4개의 교육훈련 기법간의 차이가 없다.
- 대립가설 : 4개의 교육훈련 기법간이 차이가 있다.
4개의 그룹으로 변수를 나누어 각각 그룹의 평균을 보자.
a = [66,74,82,75,73,97,87,78]
b = [72,51,59,62,74,64,78,63]
c = [61,60,57,60,81,55,70,71]
d = [63,61,76,84,58,65,69,80]
print("a 평균 : ",np.mean(a))
print("b 평균 : ",np.mean(b))
print("c 평균 : ",np.mean(c))
print("d 평균 : ",np.mean(d))
평균이 각각 다르다. 더 정확한 판단을 위해 박스플롯을 그려보자.
plot_data = [a,b,c,d]
plt.boxplot(plot_data)
plt.xticks([1,2,3,4],['a','b','c','d'])
plt.grid(True)
plt.show()
▼박스플롯 보는 법

분산분석은 F분포를 따른다. F 분포와 귀무가설 또는 대립가설 채택을 위한 Pvalue를 보자.
F_statistic, pVal = stats.f_oneway(a,b,c,d)
print('F={0:.1f},p={1:.3f}'.format(F_statistic, pVal))
p-value값이 0.05보다 작다. 따라서,
if pVal <0.05:
print("대립가설 채택")
else:
print("귀무가설 채택")
2) 이원분산분석(Two-Way ANOVA)
[ 문제 ] 다음 데이터는 당뇨병 환자와 아닌 사람들의 다양한 정보를 모은 데이터셋이다. 각 정보에 대해 당뇨병 발병과 관련이 있는지 분석해라.
▼ csv 파일
-> 두개 이상의 독립변수가 있으며, 다양한 요인들과 종속변수와의 연관성을 찾아야 한다. 따라서 이원분산분석을 사용한다.
우선 각각 요인들에 대한 정보를 파악하자.

각각의 컬럼 정보
- 정보1 (pregnant) : 과거 임신 횟수
- 정보2 (plasma) : 포도당 부하 검사 2시간 후 공복 혈당 농도 (mm Hg)
- 정보3 (pressure) : 혈압(mm Hg)
- 정보4 (thickness) :삼두근 피부 주름 두께(mm)
- 정보5 (insulin) : 혈청 인슐린 (2hour, mu U/ml)
- 정보6 (BMI) : 체질량지수 weight(kg)/(height(m)*height(m))
- 정보7 (pedigree) : 당뇨병 가족력
- 정보8 (age) : 나이
- 정보9 (class, diabetes(당뇨병), output) : 당뇨1, 당뇨0(당뇨가 아님)
데이터의 정보를 살펴보자.




단순히 정보를 봐서는 특별한 점이 없다. 한 변수를 정해서 당뇨병 발병과 비교해보자.
임신 횟수와 비교해보자.
#임신횟수 당 당뇨병 발생확률
temp = df[['pregnant','diabetes']]
temp.head(3)
임신 횟수당 당뇨병 발생 확률에 대한 평균을 구해보자.(group by)
temp1 =temp.groupby(by=['pregnant']).mean()
temp1.head()
# as_index=False 가 있으면 pregnant 변수가 살아있게 된다. 따라서 완벽한 선형을 이루게 됨.
#그래프 그리기
%matplotlib inline
temp1.plot(grid=True)

그래프를 그려보니 임신횟수가 많을수록 당뇨 확률이 높아지는 우상향 그래프를 볼 수 있다. 근데 14회 이상이 좀 이상하다. 자세히 살펴보자.

임신횟수는 우상향 그래프를 그리는 선형관계에 있으나 14회 이상인 데이터가 모두 1에 해당한다.
명확히 관련이 있다고 보기에는 근거가 부족하다.
이러한 분석을 일일히 할 수도 없기 때문에 다변량 데이터를 분석할 수 있는 라이브러리가 있다.
seaborn
matplotlib을 기반으로 좀 더 정교하게 그래프를 그릴 때 사용한다.
▼seaborn 장점
seaborn은 matplotlib 처럼 그래프를 그리는 기능이다.
matplotlip으로도 대부분의 시각화는 가능하지만 아래와 같은 이유들로 seaborn을 더 선호하는 추세이다.
1. seaborn에서만 제공되는 통계 기반 plot
2. 특별하게 꾸미지 않아도 깔끔하게 구현되는 기본 color
3. 더 아름답게 그래프 구현이 가능한 palette 기능
4. pandas 데이터프레임과 높은 호환성
: hue 옵션으로 bar 구분이 가능하며, xtick, ytick, xlabel, ylabel, legend 등이 추가적인 코딩 작업없이 자동으로 세팅된다.
각 데이터간의 상관관계를 그래프로 표시해보자.
df.corr()
상관분석 : 상관관계의 값을 파악할 수 있는 정도의 값을 상관 계수 (-1~1 사이)
0 < p ≤ 1 : 양의 상관관계 / p=0 : 상관관계가 선형적이지 않다. / -1 ≤ p < 0 : 음의 상관관계
import matplotlib.pyplot as plt
import seaborn as sns
# 1. 색상구성 결정
colmap = plt.cm.gist_heat
# 2. 크기 설정
plt.figure(figsize=(14,14))
# 3. 상관계수 출력
df.corr()
이것을 그래프가 아닌 그림으로 시각화 할 수도 있다. 히트맵(heatmap)이라고 한다.
# 히트맵 그래프 속성 결정 : vmax의 값을 0.5로 지정해서 0.5에 가까울수록 밝은색으로 표시한다.
sns.heatmap(df.corr(),linewidths=0.1,vmax=0.5,cmap=colmap,linecolor='white',annot=True)
plt.show()
그래프를 통해서 plasma 항목(공복혈당농도)가 diabetes 항목과 가장 상관관계가 높다는 것을 알 수 있다. 따라서 plasma가 결론을 만드는 가장 중요한 역할을 한다는 것을 예측할 수 있다.
당뇨병과 공복혈당농도 간의 상관관계를 좀 더 자세히 분석해보자.
- FacetGrid : 다중 플랏을 출력할 수 있다. 예를들면 그래프를 그려도 성별별로 나온다던지 등. 상관관계를 기반으로 map을 다양하게 그려보자.
grid = sns.FacetGrid(df,col='diabetes')
grid.map(plt.hist,'plasma',bins=10) #히스토그램으로 보자.
plt.show()
당뇨병에 걸린 사람(=1)의 경우 plasma가 100 이상일 때 발병률이 높다.
당뇨병에 걸리지 않은 사람(=0)의 경우 plasma가 100 가까이에 데이터가 몰려있다.(정규분포?)
[ 문제 ] seaborn에 내장된 tips 데이터를 이용해서 시간별 총 팁의 가격을 산점도로 그려보자.
산점도는 각 데이터의 관련도를 점으로 표시한다. 점의 분포도로 모양을 볼 수 있고, 이상치를 한눈에 볼 수 있으므로, 두개의 다른 변수의 연관성을 파악하는데 효과적이다.
grid = sns.FacetGrid(data=df, col='time') #row는 세로로 나온다.
grid.map(sns.scatterplot,'total_bill','tip') # 이번엔 산점도로 보자.
hue를 쓰면 색깔을 부여해서 3가지의 요인을 비교할 수 있다. 성별을 추가적으로 부여해보자.
g =sns.FacetGrid(data=df, row='time') #세로로
#hue : 설정된 변수의 값에 따라서 색상이 구별된다.
g.map_dataframe(sns.scatterplot,x='total_bill', y='tip',hue='sex')
g.set_axis_labels("Total bill","Tip") # 라벨
g.add_legend()
회귀 분석(Regression analysis)
한 개 이상의 변수를 다룰 때 특정 변수가 다른 변수와 어떤 관계를 맺는지 분석하고, 이를 바탕으로 모델을 정의해 값을 예측하는 기법. 통계적으로 데이터를 분석하는 방법 중 하나로, 입력에 대해서 연속적인 값을 대응시키는 문제이다.
회귀분석은 독립변수 X에 대해 종속변수 Y의 사이의 관계를 수학적인 모형을 이용해서 규명한다. 규명된 함수식을 이용해서 독립변수 X의 변화로부터 종속변수의 Y값의 변화를 예측한다.
회귀분석은 기본적으로 회귀모델 직선과 실제 값의 차이를 뜻하는 잔차(residual error)를 최소화 시키는 것을 기본 원리로 한다.
회귀분석은 1. 두 변수가 선형관계를 가지는 지 산점도를 작성 2. 최소자승법으로 최적의 직선식 구함 3. '선형관계가 없다'는 귀무가설을 기각할 것인지 결정하기 위한 분산분석 을 진행한다.
1) 단순선형회귀분석(simple linear regression analysis)
하나의 종속변수(y)와 하나의 독립변수(x) 사이의 관계를 분석할 경우 사용. 둘 사이의 관계를 가장 잘 설명해주는 선형함수를 찾으면, 우상향 또는 우하향하는 직선을 찾게 된다. 사실 완벽하게 들어맞는 선형함수를 찾아내는 것은 거의 불가능하지만, 최대한 x와 y의 관계를 가장 잘 설명해줄 수 있는 일차함수식을 찾아내는 것이 단순선형회귀의 목적이다.
y = wx +b -> 이 직선은 최소제곱법을 이용한 예측치와 관측치 차이의 제곱의 합이 최소가 되는 직선이다.
보통 y는 예측값(=라벨값, 구하려는 값), x는 특성이며, w는 가중치 또는 계수(coefficient), b는 편향(offset)이라 부른다. 우리는 여러 개의 샘플들의 특성값들과 라벨값들을 이용해서 가장 적합한 w와 b를 찾아야 한다. 이럴 때 사용되는 방법이 바로 경사하강법(gradient descent)이다.
경사하강법(gradient descent)
1. 임의로 설정한 일차함수와 데이터 사이의 평균제곱오차(MSE, mean squared error)를 구한다.

n은 샘플의 갯수이고,
[ 문제1 ] 윌별로 전기 생산금액(억원)에 대해 전기사용량(백만 Kw)은 어떠한 관계를 보이는가?
from scipy import stats
# 월별 전기생산 금액(억원)을 변수 x,
x = [3.52, 2.58, 3.31, 4.07, 4.62, 3.98, 4.29, 4.83, 3.71, 4.61, 3.90, 3.20]
# 이 때 전기 사용량(백만 Kw) 을 y로 한다
y = [2.48, 2.27, 2.47, 2.77, 2.98, 3.05, 3.18, 3.46, 3.03, 3.25, 2.67, 2.53]생산 금액에 대비 전기사용량을 구하고자 한다. 종속변수가 생산량에 대한 kw가 y 값이므로, y값은 연속형 변수이다.
scipy.stats.linregress(x,y)
두 세트의 측정에 대한 선형회귀분석을 호출하는 함수
단, x와 y 배열의 길이가 같아야한다.
x만 있는 경우, 한 차원의 길이가 2인 2차원 배열이어야한다.
[반환 가능한 값]
slope : 회귀선의 기울기
intercept : 회귀선의 절편
rvalue : 상관계수
pvalue : 예측기준(0.05)
stderr : 추정된 기울기의 표준 오차(표준편차)
# 반환값 -> slope : 기울기, intercept : 절편,
# rvalue : 상관계수, pvalue : 예측기준(0.05), stderr : 에러 표준편차
slope, intercept, rvalue, p_value, stderr = stats.linregress(x,y)x,y 값에 대한 정보를 변수에 부여한다.
하나씩 꺼내볼 수도 있다.
#에러 표준편차 출력
print('stderr : ',stderr)
#상관계수 출력
print('rvalue : ', rvalue)
상관계수가 0.89로 상당히 높다. 두 변수간에는 강한 양의 상관관계가 있음을 알 수 있다. (통계적으로 상관관계가 있고 유의미하다.)
pvalue 값으로 귀무가설을 확인해보자.
print('p_value : ', p_value) #0.05보다 적으면 유의미하다라고 판정
독립변수(전기생산량), 종속변수(전기소비량)
독립변수가 1개이므로 단순회귀분석(선형회귀분석)을 사용한다.
- 귀무가설 : 전기생산량과 전기 소비량간의 상관관계가 없다.
- 대립가설 : 전기생산량과 전기 소비량간의 상관관계가 있다.

선형회귀분석은 각 값에 대해 점을 찍고 회귀선(가장 손실이 적은 선)과의 거리인 '잔차'를 통해 데이터가 많아질수록 회귀선으로 회귀하는 것을 이용해서 두 변수간의 관계를 분석한다.
이를 그래프로 표시하면 명확하게 알 수 있다.
%matplotlib inline
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlim([2.5,5.0]) #x축의 시작좌표, 마지막좌표
ax.set_ylim([2.0,3.7])
#산점도 그리기
plt.grid(True)
plt.scatter(x,y)
#회귀선 그리기
#회귀선을 그리기 위해서는 numpy 배열로 변환해야한다(*****)
#회귀선 : 가장 [손실이 적은선]을 그어서 그것을 분석하는 것을 의미한다.
# 1차함수 : y=w(기울기)x + b(절편)
x1 = np.array(x)
#플롯 그리기
plt.plot(x1,slope*x1+intercept, c='red')
plt.title('단순선형회귀곡선 예제')
plt.xlabel('전기생산량')
plt.ylabel('전기사용량')
plt.show()
회귀선에 따른 값들을 계산도 해볼 수 있다.
기울기를 임의로 정해서 계산해보면 다음과 같은 결과가 나온다.

[ 문제2 ] 다음은 오존과 관련된 데이터셋이다. 온도에 따른 오존량을 예측해보고, 둘의 상관관계를 출력(시각화) 해라.
우선 데이터부터 읽어오자.
# 데이터 읽기
df = pd.read_csv('./dataset/ozone.csv')
df.head()
일단 NaN값이 보이니 지우고 시작하자.
#NaN 있는 행 삭제
df = df.dropna(axis=0)
온도에 따른 오존량을 예측하는 것이 목적이기 때문에, 독립변수는 온도, 종속변수는 오존량이 된다.
각각 x와 y 값에 넣어준다.
x = df['Temp']
y = df['Ozone']
앞선 예제처럼 정보를 변수에 부여하고 산점도를 그린다.
slope, intercept, rvalue, p_value, stderr = stats.linregress(x,y)
%matplotlib inline
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlim([57,100]) #x축의 시작좌표, 마지막좌표
ax.set_ylim([1.0,100])
#산점도 그리기
plt.grid(True)
plt.scatter(x,y)
#회귀선 그리기
#회귀선을 그리기 위해서는 numpy 배열로 변환해야한다(*****)
#회귀선 : 가장 [손실이 적은선]을 그어서 그것을 분석하는 것을 의미한다.
# 1차함수 : y=w(기울기)x + b(절편)
x1 = np.array(x)
#플롯 그리기
plt.plot(x1,slope*x1+intercept, c='red')
plt.title('단순선형회귀곡선 예제')
plt.xlabel('온도')
plt.ylabel('오존량')
plt.show()
선형인 관계를 보인다. P-value 값을 확인하고 가설을 검증하면,
print('p_value (상관계수) :', p_value) # 0.05보다 적으면 유의미하다라고 판정
if p_value < 0.05:
print("대립가설")
else:
print("귀무가설")
-> 온도가 올라갈수록 오존량이 증가하는 선형관계를 가진다.
사이킷런(scikit-learn)
분류, 회귀, 군집화, 의사결정트리 등 다양한 머신러닝 알고리즘을 적용할 수 있는 라이브러리. 기본적인 샘플데이터를 포함하고 이어 데이터셋 모듈을 읽어들여 로드가 가능하다.
print(데이터셋이름.DESCR) 을 하면 데이터셋의 정보를 볼 수 있다.
데이터를 다루기 쉽게 하기 위해 pandas의 데이터프레임으로 변환시켜서 많이 사용한다.
▼사이킷런 라이브러리 설치
!pip install mglearn
[ 문제3 ] 사이킷런의 Boston 데이터셋을 받아서 데이터 셋 나눠서 훈련시켜보기
설치한 사이킷런에서 데이터셋을 로드하고 회귀분석을 준비한다.
#사이킷런
import mglearn
#사이킷런에서 제공해주는 보스턴 집값에 대한 데이터셋을 제공
from sklearn.datasets import load_boston
#회귀분석을 하기 위한 패키지
from sklearn.linear_model import LinearRegression
# 학습용 검증용 데이터 셋을 나누기 위한 패키지
from sklearn.model_selection import train_test_split편의성을 위해 boston이라는 이름의 변수로 사용한다,.
#변수에 저장
boston = load_boston()
#레이블 이름 출력
boston.feature_names
#보스턴 데이터셋 설명 보기
print(boston.DESCR)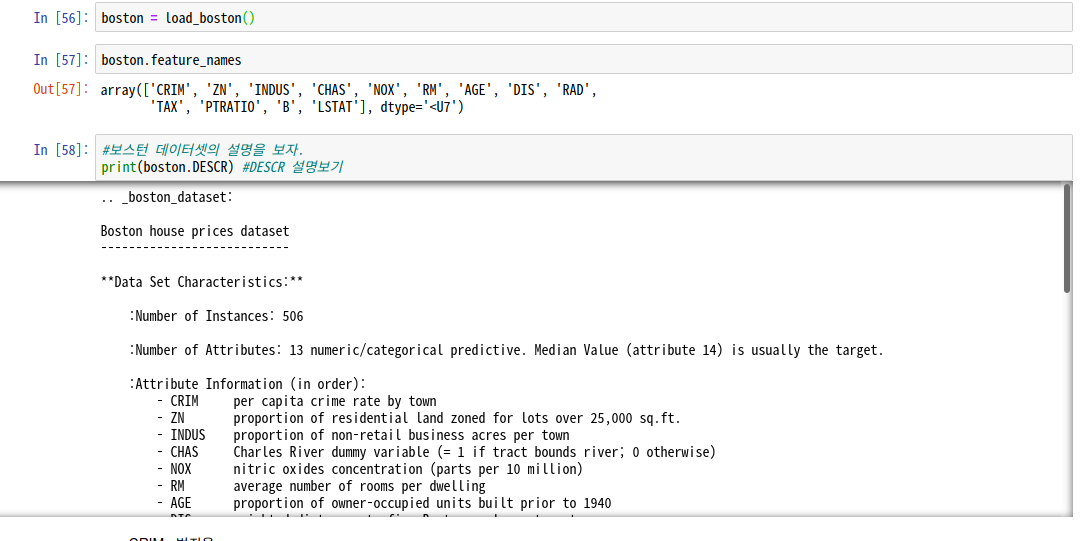

이미지 출처: http://dator.co.kr/?vid=ctg258&mid=textyle&document_srl=1721307
보스턴 데이터셋을 pandas의 dataframe으로 변환한다.

'[ Python ]' 카테고리의 다른 글
| [Python] 머신러닝 개념 잡기 (1) | 2020.11.06 |
|---|---|
| [Python] SciPy / 기초기술통계 / 카이제곱검정 / T검정 (0) | 2020.10.30 |
| [Python] Pandas 기초 / groupby / 데이터프레임 Json으로 저장 / 실습(3) (0) | 2020.10.30 |
| [Python] Pandas 기초 / DataFrame / matplotlib / 실습(2) (0) | 2020.10.29 |
| [python] 주피터 노트북(jupyter notebook) 단축키 (0) | 2020.10.28 |